Współczynnik dwumianowy – Symbol Newtona C#

Współczynnik dwumianowy – Symbol Newtona C#

Czym jest nazywany w dwojaki sposób Współczynnik dwumianowy – Symbol Newtona?

Czasem zdarza się sytuacja, w której potrzebujemy wyznaczyć ilość kombinacji elementów danego zbioru. Jest to sytuacja, która wbrew pozorom zdarza się bardzo często, ale nie zawsze istnieje konieczność dokonywania obliczeń, a decyzje podejmowane są intuicyjnie.

Dla przykładu rozpatrzyć można kilka sytuacji, w których dokonywany jest wybór uwzględniający ilość kombinacji:

– Ukazała się seria 4 kolekcjonerskich kart znanych sportowców, a my możemy pozwolić sobie zaledwie na 2 z nich. Z takiego zestawu możemy wybrać karty o numerach {1,2}, {1,3}, {1,4}, {2,3}, {2,4}, {3,4}, a więc możemy dokonać aż 6 różnych wyborów.

– Ulubiona gra liczbowa losuje 5 niepowtarzających się liczb z 60 dostępnych. Ilość kombinacji jest znacznie większa niż w poprzednim przykładzie i wypisanie wszystkich zajęłoby sporo miejsca w tym artykule.

– Firma zatrudnia 100 pracowników, a połowa z nich otrzyma w tym miesiącu premię. Ile kombinacji wyboru pracowników może tu się wystąpić? Wielu pracodawców nie zastanawia się nad tym i robi podział wg własnego uznania.

Definicja Symbol Newtona

Co, gdy jednak chcielibyśmy przekonać się, ile mamy tak na prawdę możliwości wyboru oraz jakie one są? Wtedy skorzystać można z wzoru zdefiniowanego przez Newtona, zwanego Symbol Newtona lub współczynnikiem dwumianowym. Jest to funkcja dwóch argumentów będących nieujemnymi liczbami całkowitymi. Rozwiązaniem Symbolu Newtona jest informacja ile możliwych kombinacji wyboru można uzyskać wybierając k elementów ze zbioru n-elementowego. Definicja wzoru wygląda następująco:

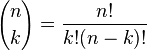
Wynik Symbolu Newtona w kodzie

Przedstawiony kod, reprezentuje rozwiązanie powyższego wzoru, bez korzystania z rekurencji dla silni. Zastosowano w nim zależność, która powstaje w momencie skrócenia wartości będącej częścią licznika z większą z liczb w mianowniku. Objaśnienie na konkretnym przykładzie powinno rozwiać wątpliwości. Licznik w Symbolu Newtona zawszę będzie większy lub równy mianownikowi. Wybierając n=8 oraz k=5 otrzymujemy ułamek:

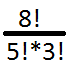
Zmienna, którą chcemy umieścić w warunku, musi być zadeklarowana przed wystąpieniem pętli w kodzie. Inicjacja zmiennej może pojawić się dopiero w pętli, ponieważ będzie to nadal przed sprawdzeniem warunku.

Skracając licznik (8!) z większym czynnikiem z mianownika (5!) otrzymamy:

– w liczniku 6 * 7 * 8 (ponieważ 1*2*3*4*5 zostanie skrócone),

– w mianowniku 1*3! (a więc 1*2*3).

W poniższym kodzie liczba 1 mnożona jest przez kolejne wartości licznika (6*7*8) i dzielona przez kolejne elementy mianownika (1*2*3). Ta zależność upraszcza zapis oraz działanie kodu do jednego warunku i jednej pętli.

long WyliczIloscGrup(long n, long k)//zwraca ilość kombinacji
{
   if (k > n - k)
      k = n - k;
   long liczGrupy = 1;
   for (int i = 0; i < k; i++)
   {
      liczGrupy = liczGrupy * (n - i);
      liczGrupy = liczGrupy / (i + 1);
   }
   return liczGrupy;
}

Grupy kombinacji w kodzie

Czasem informacja o ilości możliwych kombinacji wyboru jest niewystarczająca i chcielibyśmy dowiedzieć się z jakich elementów się one składają. Kod jest stosunkowo prosty w przypadku, gdy znana jest nam ilość elementów, która ma zastać wylosowana oraz ile jest ich dostępnych. Sytuacja komplikuje się gdy funkcja ma być uniwersalna i użyteczna dla dowolnych wartości.

Poniżej przedstawiono kod funkcji, która pobiera przedstawione wcześniej parametry n oraz k, a zwraca tablicę tablic. Zwracana tablica w każdym wierszu przechowuje tablicę jednoelementową z wartościami należącymi do danej grupy. Wiersze można więc interpretować jako kolejne grupy, a ich kolumny jako wylosowane w nich elementy.

Algorytm wymaga wyjaśnienia, ale żaby lepiej go zrozumieć posłużę się przykładem n=6, k=4.

Definiowanie wylosowanych wartości odbywa się w pętli while. Pierwsze jej wywołanie zapisuje pierwotnie zdefiniowaną grupę (1,2,3,..,k – w naszym przykładzie 1,2,3,4). Kolejne wywołania pętli zwiększają ostatni element w pierwotnej tablicy, aż do wystąpienia na nim wartości maksymalnej, równej n (czyli -> 1,2,3,5 -> 1,2,3,6). Po wystąpieniu takiej wartości, zmienna p jest zmniejszana o 1, co powoduje odwołanie się do elementu o niższym indeksie (na tym etapie jest to wartość z 3 pozycji równa 3, która zostaje zmieniona na 4). Elementy z większymi indeksami od niej są zwiększane o 1, względem nowej zmiennej (1,2 pozostają bez zmian, 4 zmienione przed chwilą i kolejne elementy 4+1=5, co daje kolejną grupę 1,2,4,5), a zmienna p znów otrzymuje wartość równą k, tak by odwoływać się do ostatniego elementu.

Odwoływanie się do elementów z coraz mniejszymi indeksami realizowane jest wtedy gdy ostatni element przyjmuje maksymalną wartość więcej niż raz, dla następujących po sobie elementów (np. pierwszy raz dla grupy 1,2,4,6 gdzie p zmniejszana jest do 3, drugi raz 1,2,5,6 gdzie p zmniejszana jest do 2). Ostatnie grupy zmniejszają zmienną p do 0 i dzięki temu oraz licznikowi wiemy, że jest to ostatnia z możliwych kombinacji.

//Wyznaczanie grup k-elementowych ze zbioru n-elementowego
int[][] WyznaczGrupy(int n, int k)
{
    int i = 0, p = 0, licznik = 0;
    //ilość możliwych grup liczb - ilość wierszy w tablicy
    long iloscGrup = WyliczIloscGrup(n, k);
    //deklaracja tablicy k-elementowej dla pojedynczych grup
    int[] pojedynczaGrupa = new int[k];
    //deklaracja tablicy tablic dla wszystkich grup
    int[][] wszystkieGrupy = new int[iloscGrup][];
    //dla każdego wiersza przypisana zostaje pusta tablica jednowymiarowa, k-elementowa
    for (i = 0; i < iloscGrup; i++)
        wszystkieGrupy[i] = new int[k];
    //uzupełnienie tablicy k-elementowej wartościami od 1 do k
    for (i = 1; i <= k; i++)
        pojedynczaGrupa[i - 1] = i;

    //losujemy mniej liczb niż mamy dostępnych (n)
    if (k < n)
        p = k;
    //wszystkie n-licz zostaje wylosowanych
    else
        p = 1;

    //Licznik - numer aktualnie uzupełnianej grupy
    while (licznik < iloscGrup)
    {
        //gdy ostatni element grupy jest równy ostatniej dostępnej wartości -> ostatni przypadek
        if (pojedynczaGrupa[k - 1] == n)
            //p jest pozycją w pierwotnie zdefiniowanej tablicy k-elementowej, do której skaczemy 
            //by zwiększyć jej wartość o jeden i wg niej ustawić kolejne elementy.
            p--;
        else
            p = k;

        //jeżeli (p>0) przekracza zakres zdefiniowanych grup i (licznik != 0) nie jest to pierwsza grupa
        if ((p > 0) && (licznik != 0))
        {
            for (i = k; i >= p; i--)
                pojedynczaGrupa[i - 1] = pojedynczaGrupa[p - 1] + i - p + 1;
        }

        //przypisanie utworzonej pojedynczej grupy do odpowiedniego wiersza w zbiorze wszystkich grup
        for (int j = 0; j < k; j++) //uzupełnianie kolejnego wiersza
            wszystkieGrupy[licznik][j] = pojedynczaGrupa[j];

            licznik++;
    }
    return wszystkieGrupy;
}

Wyświetlanie wszystkich kombinacji

Poniżej został zaprezentowany kod, zbierający w zmiennej string dane dotyczące składu grup i ich numeracja w sposób przyjemny dla ludzkiego oka:

1  –  1 2 3 4 5
2  –  1 2 3 4 6
3  –  1 2 3 4 7
4  –  1 2 3 4 8
….

//Wyświetlanie 
int line = 0;
licznik = 0;
while (licznik < iloscGrup)
{
   line++;
   wyswietlwszystkieGrupy += "\n";
   wyswietlwszystkieGrupy += line.ToString();
   wyswietlwszystkieGrupy += "  -  ";

   for (int j = 0; j < k; j++) //uzupełnianie kolejnego wiersza
      wyswietlwszystkieGrupy += wszystkieGrupy[licznik][j].ToString() + " ";
   licznik++;
}